What Does Air Mass Have To Do With Sunlight?

Definition of Air Mass

When you first read the term “air mass” you might have wondered what relevance the mass of air has with sunlight and the solar spectrum. You’re not alone! It’s a term that can definitely cause some confusion, but is very important for understanding the way different solar spectra are defined. It’s doubly confusing because there are similar definitions in the disciplines of meteorology and solar energy.

In meteorology, air mass is defined as a volume of air with a specified temperature and vapor content. Two similar air masses will therefore have gases and particles exhibiting similar chemical and spectral behaviour. This is not the definition that’s most useful in the discipline of solar energy.

In the solar energy field, air mass is better referred to as “air mass coefficient” and defines how much atmosphere there is between you and the Sun. As we discussed earlier, the atmosphere absorbs and scatters light, so how much of it is vital to knowing and quantifying the spectrum of light. The air mass coefficient tells you the relative distance (or path length) that light has to travel through the atmosphere before it gets to you.

While these two definitions share some similarities, it is important to recognize that they are not interchangeable. Therefore, when you’re in solar energy circles, the term “air mass” really refers to “air mass coefficient.” We’ll go through some specific examples below.

What is the AM0 Spectrum?

Earlier, we described how the sun’s emission spectrum can be closely approximated by a 5800 K black body. This emitted radiation travels 150 million kilometers and arrives at Earth’s orbit. Because it has traveled through the vacuum of space, there were no particles to absorb or scatter the light.

What is the air mass coefficient of such a spectrum? To answer that, we first must answer: how much atmosphere has the light traveled through?

The answer, in this case, is none—zero. There’s been no atmospheric transmission whatsoever.

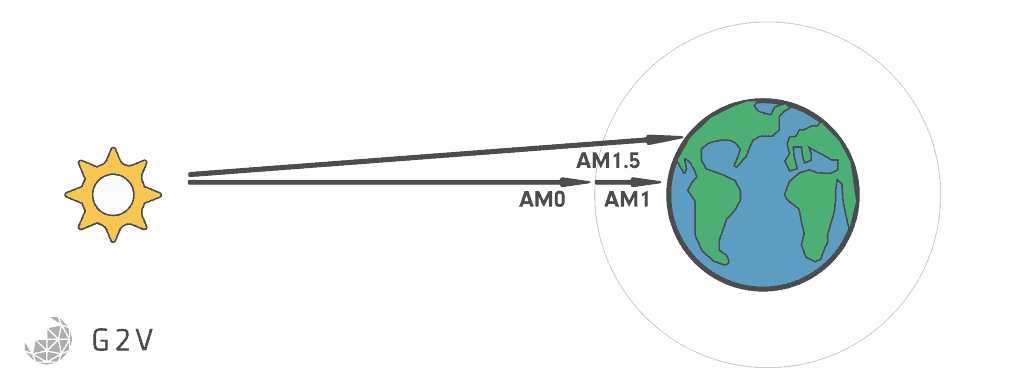
This spectrum is what we call Air Mass 0 (AM0), indicating the sunlight has not interacted with any of the Earth’s atmosphere.

Next, we’ll discuss examples of spectra that have passed through the Earth’s atmosphere.

What is the AM1 Spectrum?

When we measure the solar spectrum on Earth, it is different from the 5800 K black body radiation of AM0 due to scattering (of blue light, for example) and absorption (of red light, for example) by molecules in the Earth’s atmosphere. Overall, the spectrum is going to be attenuated or diminished after passing through air. The more atmosphere sunlight passes through, the greater the light’s attenuation.

We’ve already discussed how air mass (or air mass coefficient) is the path length of a direct sunbeam through the atmosphere. Now we can introduce some definitions and specifics of how to calculate it.

The air mass coefficient defines “1” as the path length light travels through when the Sun is directly overhead at sea level. The spectrum of light after travelling through this path length of atmosphere is what we call Air Mass 1 or AM1. In this case, the sun’s direct radiation passes vertically through the atmosphere in the shortest possible path.

This point directly above a particular location is known as the zenith. expressed as a ratio relative to the sun at the zenith (a zenith is an imaginary point directly above a particular location) above a sea-level location. In this case, the sun’s direct radiation passes vertically through the atmosphere in the shortest possible path. This is known as Air Mass 1.

AM1 is the baseline from which the rest of the spectra can be defined. Air mass is expressed as a ratio relative to the sun at the zenith above a sea-level location.

If we have twice the path length as that of seaside sunlight zenith, then that spectrum is referred to as AM2. If we have four times the path length, that’s AM4, and so on.

What are the AM0.1, AM0.2 … AM0.9 Spectra?

These spectra refer to fractions of the standard path length when the sun is at its zenith shining on the sea. If you climb up a mountain until you are at half the atmosphere’s height, the light when the sun is directly overhead will be travelling through half the path length, and you’ll be exposed to the AM0.5 spectrum. If you fly a plane until you’re at 90% of the height of the atmosphere’s height, with only 10% remaining, then the plane will be exposed to AM0.1 (i.e. 10% of the path length of AM1).

Because we have topography and don’t spend all our time at sea level, we need spectral definitions for when the sun is directly overhead, and we’re above the sea. These are all the spectra from AM0.1 to AM0.9.

What are the AM1.1, AM1.5, AM2, AM5… AM40 Spectra?

These spectra correspond to sunlight that has traveled through path lengths much longer than direct overhead sunlight at sea level (1.1 times, 1.5 times, 2 times, 5 times, and 40 times to be specific).

Your next question might be: when does light travel through that path length? For that, we’ll need to do some calculations, but the short answer is that as the sun changes its angle on the horizon, the AM spectrum changes.

When does a Specific AM Spectrum Apply?

Because the air mass coefficient is calculated as the ratio of the sun’s actual path length to that at the sun’s zenith, we can use some basic geometry to start seeing when AM1.1, AM1.5, etc. might actually apply.

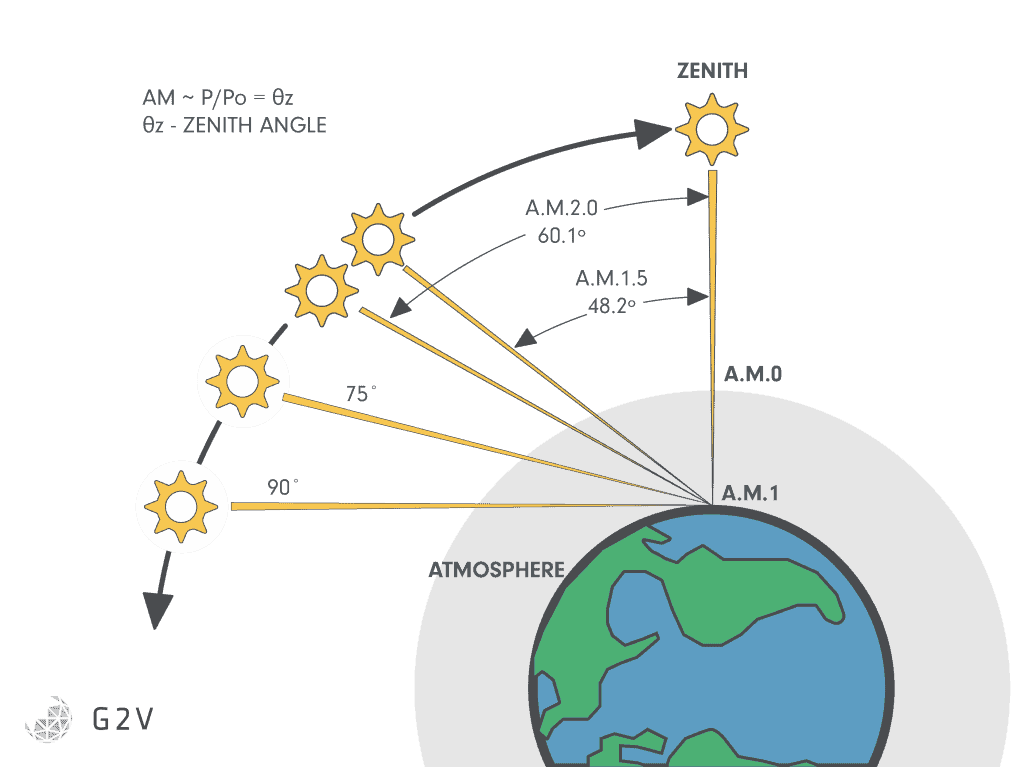
The fundamental thing that’s changing when the air mass coefficient changes is the zenith angle; that is, the angle between the sun’s current position and a line directly overhead. The higher the zenith angle, the lower the sun is in the sky, and the more atmosphere sunlight has to travel through.

To know when a specific AM spectrum applies then is really a question of figuring out what the sun’s zenith angle for that AM spectrum really is.

How Do I Calculate Zenith Angle from the Air Mass Coefficient?

The easiest way (to first-order) to relate Zenith angle and the air mass coefficient is to use simple triangles. 

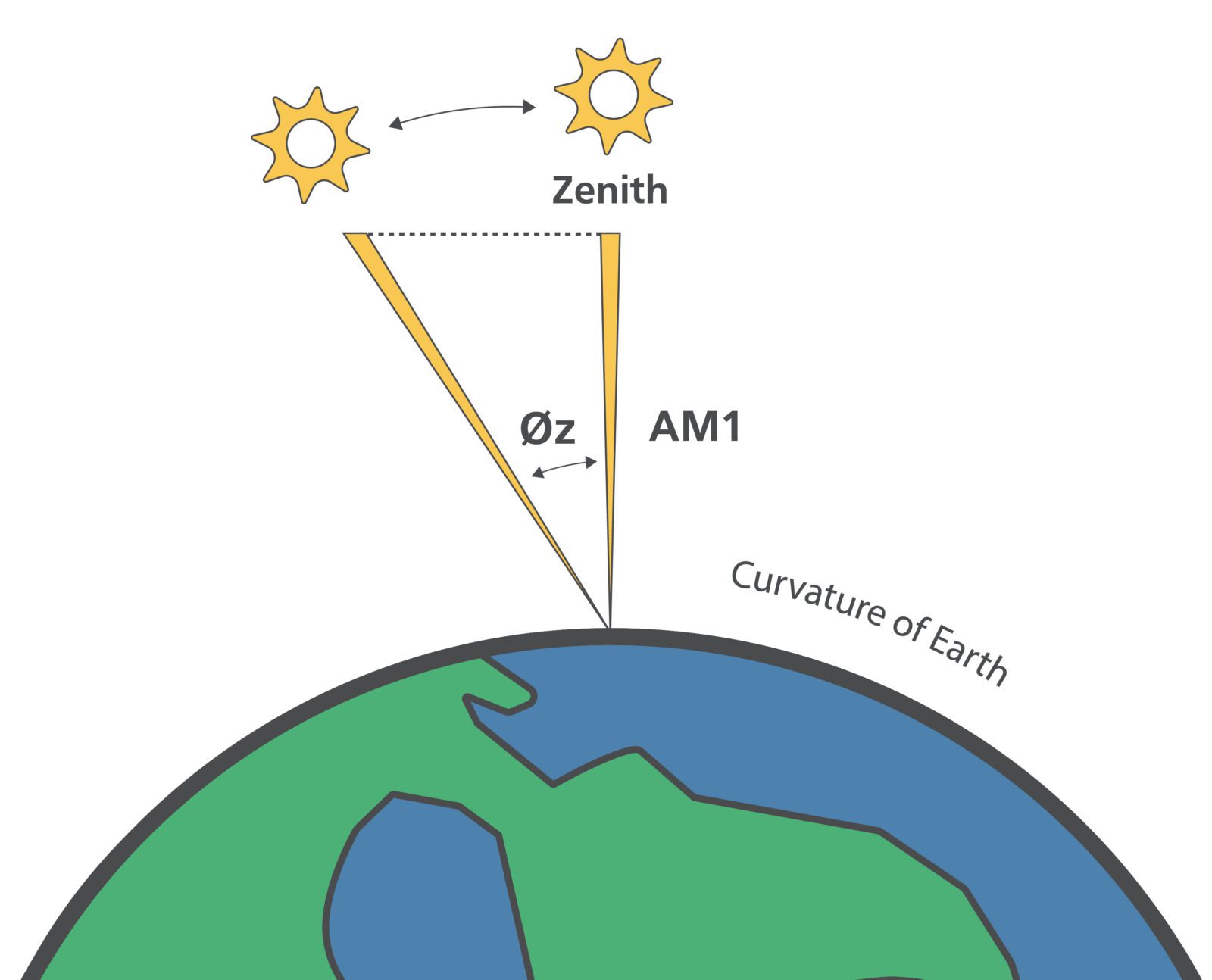
In this case, trigonometry gives us our equation:

This equation tells us that we’ll get an Air Mass of 1.1 at a zenith angle of about 25 degrees, an Air Mass of 1.5 at about 48 degrees, AM2 at about 60 degrees, and AM40 at 89 degrees. There are a few inaccuracies with this simple calculation, though, as the diagram below shows.

The simple-triangle example doesn’t take into account the curvature of either the Earth or its atmosphere. The simple triangle approximation is reasonably accurate up to around 75 degrees, but overestimates air mass at high zenith angles. There are a number of approximations that provide a better estimate of air mass across the full range of zenith angles, some even including the effects of atmospheric refraction (for example, in the open ocean, the sun is visible before it has risen above the horizon, because light has been bent by the atmosphere around the curve of the earth).

Unfortunately, these models generally go from zenith angle to air mass, and are not easy to solve going in the reverse direction. If you have to go from Air Mass to zenith angle, we recommend using the simple triangle as a rough estimate, then iteratively finding a more accurate solution using the models we discuss in the next section.

How Do I Calculate the Air Mass Coefficient From Zenith Angle?

The simple triangle model makes it easy to go from zenith angle to AM or vice versa, interchangeably:

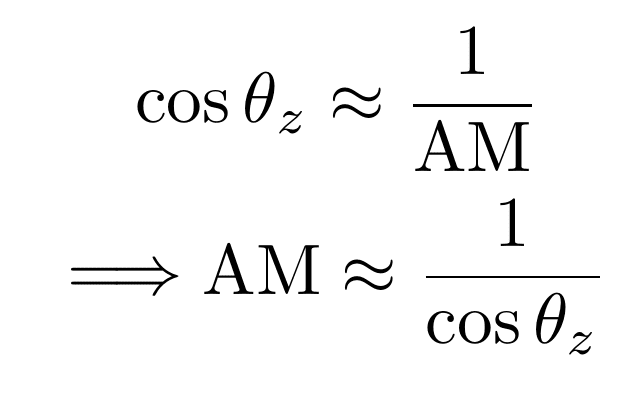
However, as discussed in the previous section, this approximation breaks down for higher angles.

Another model (by Kasten & Young, 1989) more sophisticated than the simple triangle model provides a more accurate estimation of the air mass coefficient. It is as follows, where theta-z is in degrees. You can plug zenith angle values directly into this model to get an accurate calculation of the relative path length increase.

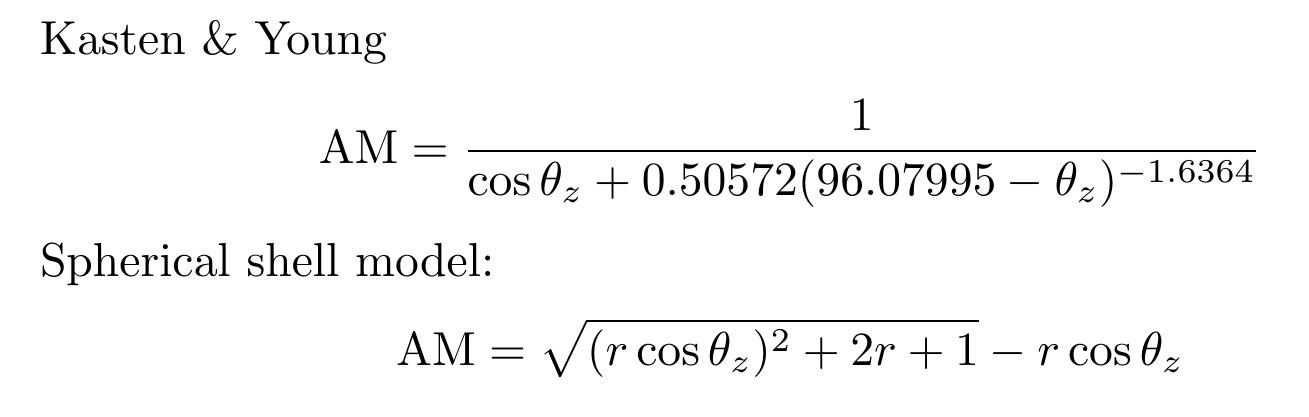
Using this will get you an air mass coefficient with high accuracy up to the maximum 90 degree zenith angle, which is far better than the simple triangle model. The disadvantage of this model is that it is difficult to solve the equation in the reverse direction, i.e. going from AM and determining the zenith angle. However, in the majority of applications this direction of calculation is not needed, and if it is, then using the simple triangle method followed by a few iterations on the above equation will get you the answer you need.

Why is AM1.5G the Standard Sun Spectrum?

Because most major population centers of the world (Europe, China, Japan, the United States, northern India, southern Africa and Australia) lie in mid-latitudes, an AM number that represents mid-latitudes is the most commonly used to characterize the performance of solar cells. AM1.5 atmosphere thickness represents a zenith angle of z=48.2°.

During the summer months, the AM number for mid-latitudes is less than 1.5, and higher figures apply during the morning and evening. Therefore, AM1.5 is a useful representation of the atmosphere thickness as a yearly average for mid-latitudes. This air mass of 1.5 was selected as the standard spectra in the 1970s for standardization purposes based on a solar radiance analysis in the United States.

The “G” in AM1.5G stands for “global,” and is the first of the suffixes that add more information and specificity to the spectra.

What are the AM1.5, AM1.5G, AM1.5D Solar Spectra?

There are a few suffixes added to the AM-specified spectra, and they take into account different effects to maximize the specificity of a spectrum. This extra level of detail makes it easier for researchers around the world to compare their results to one another by ensuring that all aspects of sunlight behaviour are considered and called out.

The “D” in AM1.5D stands for directed, and corresponds to sunlight that directly shines on a point on Earth (i.e. with no reflections or scattering).

AM1.5G corresponds to a global spectrum that includes diffuse and scattered light. It also specifies that it’s considering light that will be received by a 37 degree tilted surface (which, when atmospheric curvature and vertical density profile are taken into account, corresponds to the solar zenith angle of 48.2 degrees mentioned above).

What Spectra are the Most Commonly Used in Testing?

Standard spectra include AM0, AM1.5G, AM1.5D. These are defined by ASTM E490, ASTM G173-03 and other standards bodies in an effort to provide standard test conditions so that experiments and results can be compared, and get a reasonable approximation for real-world performance. AM0 and AM1.5G are by far the most commonly used test spectra.

The spectrum generated by sunlight at AM1 (at 0° from the zenith) to AM1.1 (at 25° from the zenith) is a useful range for estimating the performance of solar cells in equatorial and tropical regions.

Other AM values are used to approximate sunlight at regions other than mid-latitudes or at higher elevations. AM2 and 3 (z=60° and z=70° respectively) for example, are useful to determine the solar performance of some devices (e.g. solar cells) at higher latitudes such as those in northern Europe. An AM value of 40 is typically regarded as being the air mass value of the horizontal direction (z=90°) at the equator.

We’ve summarized a few example air masses and their properties in the table below.

Some example Air Mass (AM) spectra and their properties.