Chapter 8
There are many different models to account for the physics driving the behavior of solar cells. We’ll start with the most basic first, and work our way toward increasing complexity.
Before we go too far, it’s worth specifying what we’re after in all of these models. Solar cell designers are inspecting the fine details of an I-V curve, which means they’re carrying out a non-linear optimization problem. Any parameters that we calculate have to match reality, be robust and repeatable, and give us similar measurements for slightly different data sets, all while taking a minimum time to compute.
There’s a trade-off between accuracy and simplicity, however. A simple model is what we started out with, but as we saw, for example, with the solar cell represented by a single diode, it couldn’t account for all the physical effects. The more complex the model, however, the more difficult it is to calculate, as well as to convey to other researchers.
Broadly speaking, there are 3 main approaches for determining the model parameters of a solar cell. The first is an analytical method, which uses the IV curve data to generate the parameters. Those types of methods are the ones we’ll be focusing on. They often involve approximations that can be inaccurate, or produce equations that are transcendental and extremely difficult to solve.
Another approach for determining model parameters involves parameter estimation and optimization. It is called a metaheuristic method because it tries to find the model parameters practically (i.e. heuristically or iteratively) while applying some intelligence and optimization (which adds the meta part). An example of a metaheuristic approach is a genetic algorithm modelling the solar cell as an artificial bee colony (don’t worry if this sounds very abstract—you’re not alone!). There are many, many other metaheuristic models.
The third approach to determining model parameters is a mixture of analytical and metaheuristic methods, trying to combine the best of both: the simplicity of the analytical methods with the power of the metaheuristic methods.
All told, there are a tremendous number of existing models (summarized in the table below), which are a testament to the creativity and ingenuity of the many researchers contributing to the field.
List of acronyms for various models and algorithms to determine PV cell parameters, taken from Abbassi et al., 2018.
ABCO Artificial Bee Colony Optimization
ABSO Artificial Bee Swarm Optimization
AE Absolute Error
AGA Adaptive Genetic Algorithm
AIS Artificial Immune System
ANN Artificial Neural Network
APE Absolute Power Error
APSO Particle Swarm Optimization with Adaptive Inertia Weight
APVE Absolute Power and Voltage Error
BBO Bio-Geography Based Optimization
BBO-M Bio-Geography Based Optimization with Mutation
BFA Bacterial Foraging Algorithm
BMO Bird Mating Optimization
BPFPA Bee Pollinated Flower Pollination Algorithm
CPSO Chaos Particle Swarm Optimization
CPU Central Processing Unit Control
DDM Double Diode Model
DE Differential Evolution
DEIM Differential Evolution with Integral Mutation
GA Genetic Algorithm
GGHS Grouping Based Global Harmony Search
GOTLBO Generalized Oppositional Teaching Based Learning
HS Harmony Search
IADE Improved Adaptive DE
IAE Individual Absolute Error
IBCPSO PSO with Inverse Barrier Constraints
IGHS Improved Global Harmony Search
IGHS Innovative Global Harmony Search
IP Interior Point
IPSO Improved Particle Swarm Optimization
ISDM Improved Single Diode Model
JADE Adaptive Differential Evolution
LM Levenberg-Marquardt
LS Least Square
MDDM Modified Double Diode Model
MPCOA Mutative-Scale Parallel Chaos Optimization
MSE Mean Squared Error
N.E. Not Extracting
NMS Nelder-Mead Algorithm
NOCT Nominal Operating Cell Temperature
NR Newton-Raphson Optimization
PDE Penalty based DE
PS Pattern Search
PSA Parallel Swarm algorithm
R-JADE Repaired Adaptive Differential Evolution
RADE Repaired Adaptive Differential Evolution.
RMSE Root Mean Squared Error
SA Simulated Annealing
SBMO Simplified Bird Mating Optimization
SDM Single Diode Model
SIV Suitability Index Variable
SSE Sum of Squared Errors
STLBO Simplified Teaching Learning Based Optimization Strategies
TDM Three Diode Model-STC: Standard Test Conditions
TLBO Teaching Learning Based Optimization
TVIWAC-PSO Particle Swarm Optimization with Time-Varying Inertia Weight and Acceleration Coefficients
VC-PSO Particle Swarm Optimization with Velocity Clamping
An overview of the various models and algorithms used to determine PV cell parameters, taken from Abbassi, R., Abbassi, A., Jemli, M., & Chebbi, S. (2018). Identification of unknown parameters of solar cell models: A comprehensive overview of available approaches. Renewable and Sustainable Energy Reviews, 90(February), 453–474. doi.org
We’ll be primarily focusing on analytical methods, since those are the ones easiest to understand, as well as the ones that G2V offers with its reference cells and IV software. However, if you have a model you’d like to see us include in our software, let us know and we’ll include the model along with appropriate citations to not only give appropriate credit where it is due, but to let other researchers know how they can get in touch to collaborate toward more refined solar cell models. Be sure to get in touch if you have a model you’d really like to see in our software. Let us help bridge the gap and get your model out among other researchers!
One-Diode Model with Shunt and Series Resistances
The following method is taken from Phang, Chan & Phillips’ 1984 paper entitled “Accurate analytical method for the extraction of solar cell model parameters,” published in Electronics Letters.
We start with the single-diode equation and include both a shunt and series resistance (we derived this earlier). However, we make the following definition to make the equation easier to write:

The diode equation becomes:
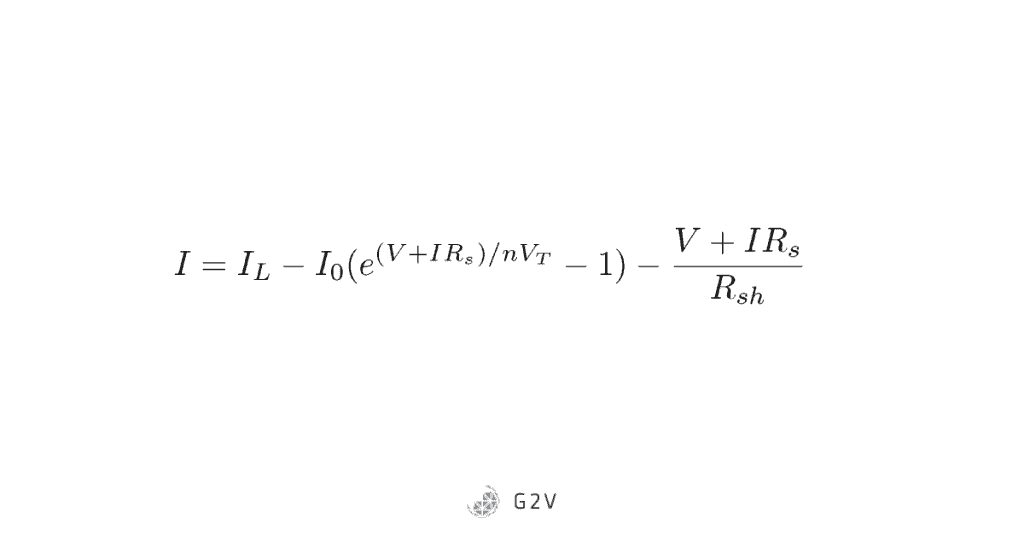
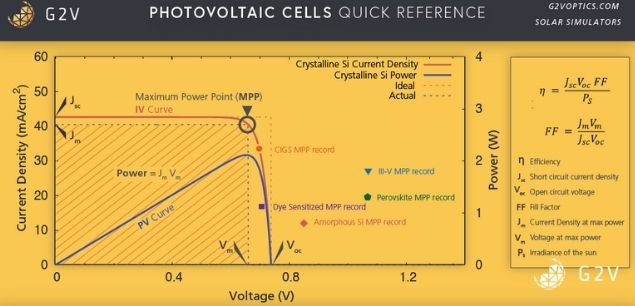
We can find the circuit parameters from the graph of the IV curve as shown below:
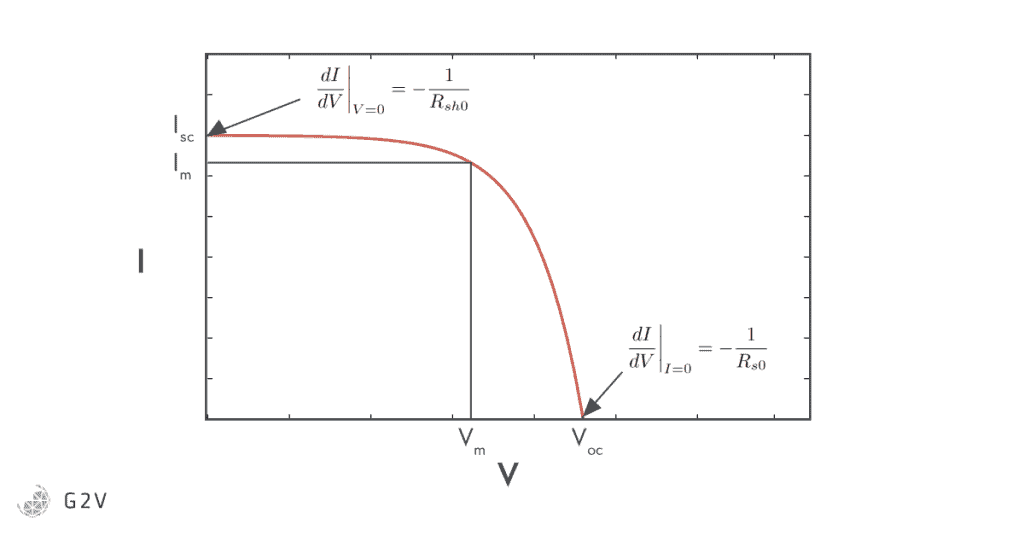
In words, the shunt resistance is related to the slope of the IV curve at V = 0, and the series resistance is related to the slope of the curve at I=0. The analytical solutions for all the parameters are then as follows:
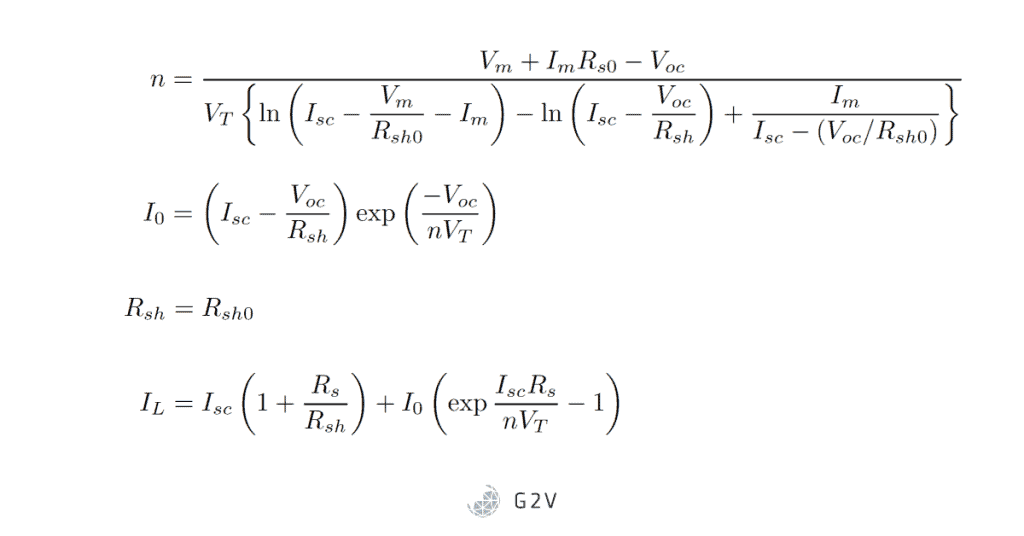
Two-Diode Model with Shunt and Series Resistances
The following method is taken from Chan & Phang’s 1987 paper entitled “Analytical Methods for the Extraction of Solar-Cell Single- and Double-Diode Model Parameters from I- V Characteristics,” published in IEEE Transactions on Electron Devices. This model includes the physics of recombination as a second diode.
We start with the two-diode equation that includes both a shunt and series resistance (we derived this earlier). However, we make the following definition to make the equation easier to write:

The diode equation becomes:
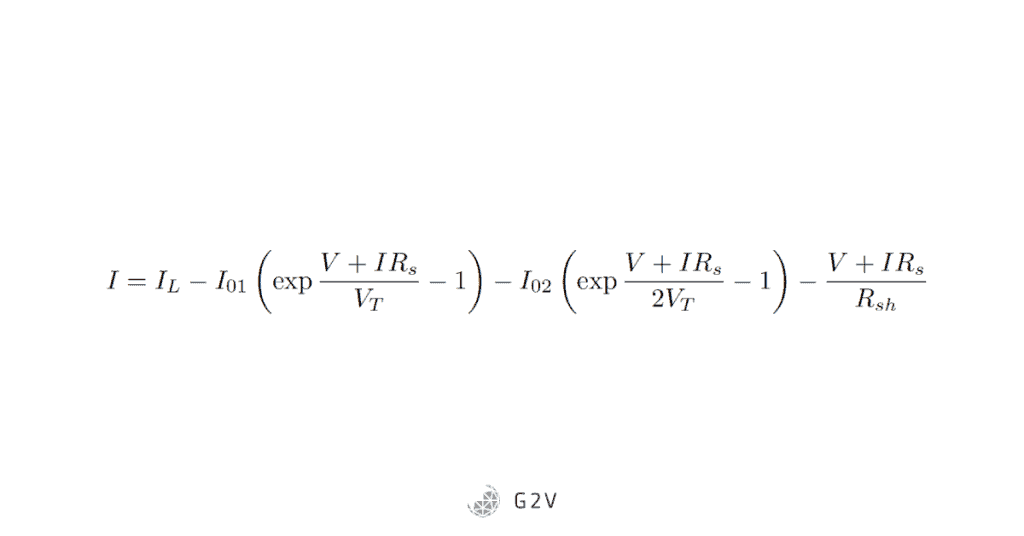
As in the one-diode model, we can find the circuit parameters from the graph of the IV curve as shown below:

In words, the shunt resistance is related to the slope of the IV curve at V = 0, and the series resistance is related to the slope of the curve at I=0. The analytical solutions for this two-diode model are considerably more complex, requiring additional parameter definitions:
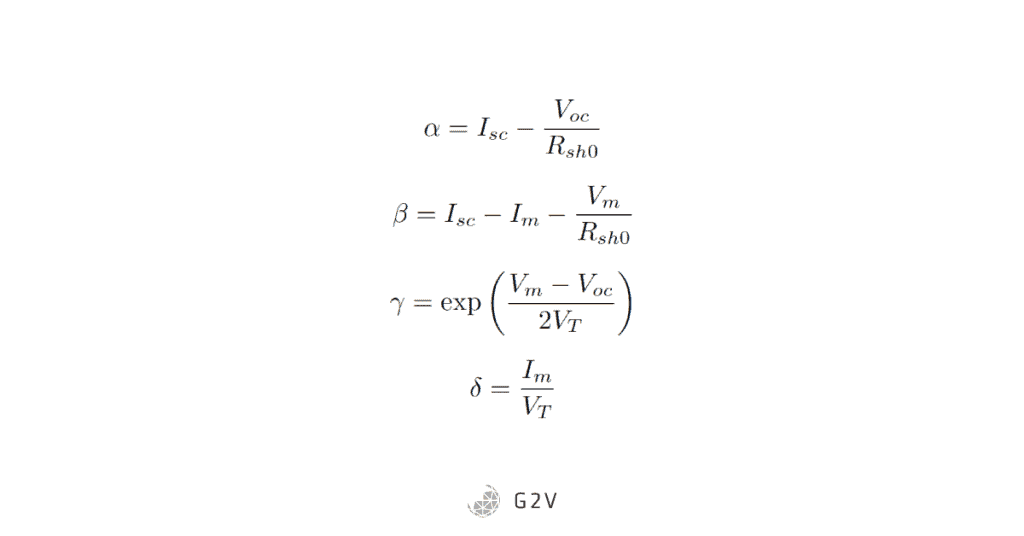
The first approximate solution can be obtained from the following quadratic equation:
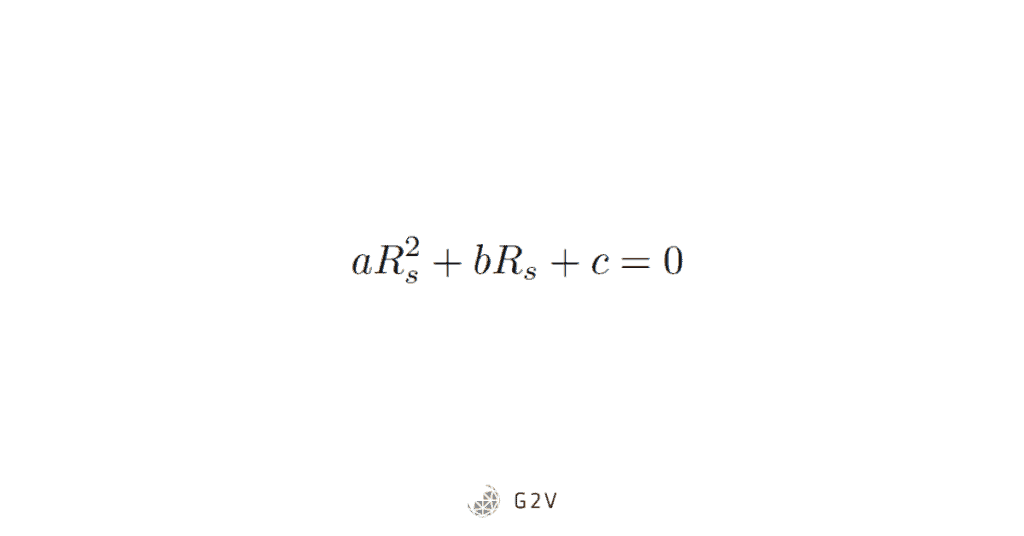
Where a, b and c are defined as
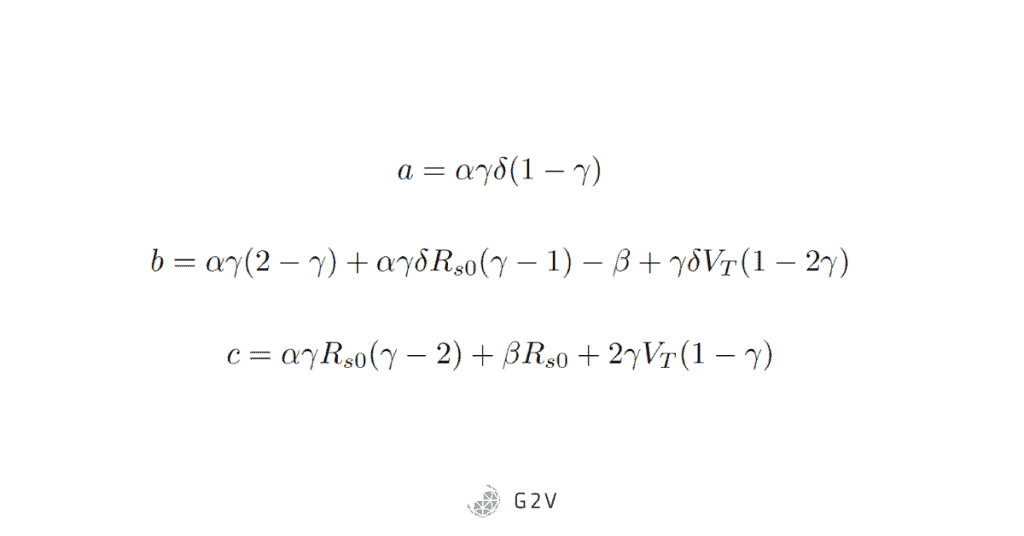
The series resistance can then be obtained by the solution to the quadratic equation:
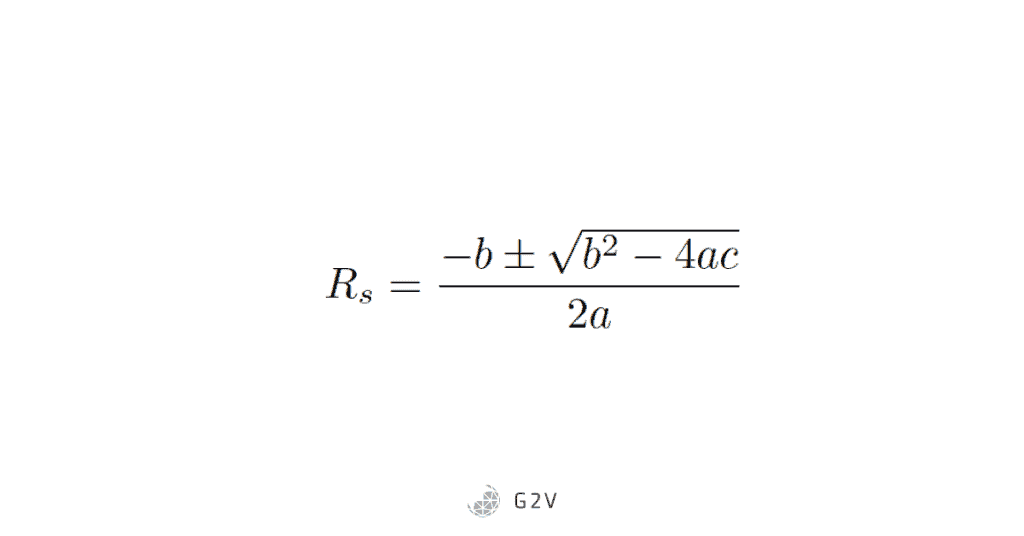
A more accurate solution, that includes more terms from the initial diode equation, results in a cubic equation as follows:

Where A, B, C and D are defined as
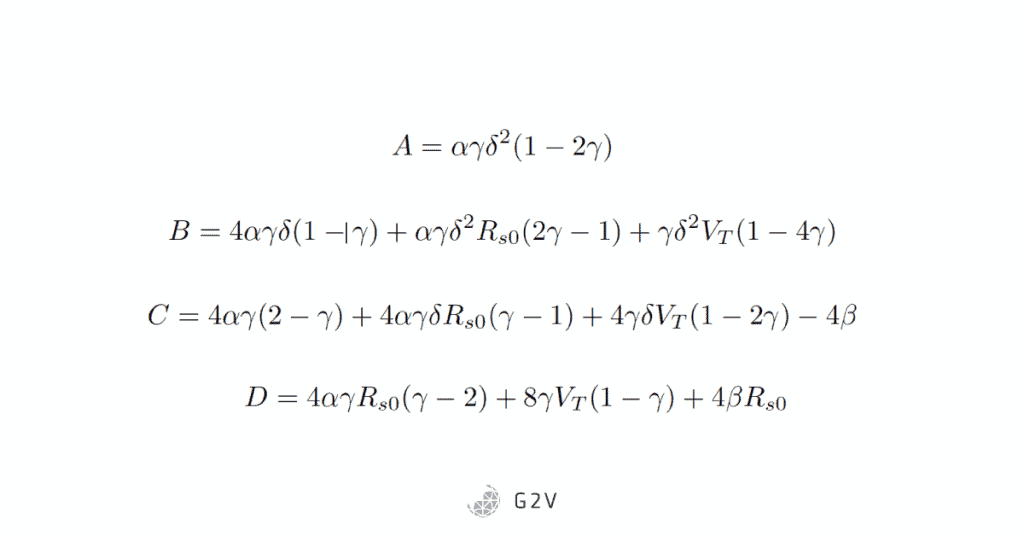
Regardless of whether the cubic or the quadratic solutions are used to determine the series resistance, the rest of the parameters can be determined from the following equations:
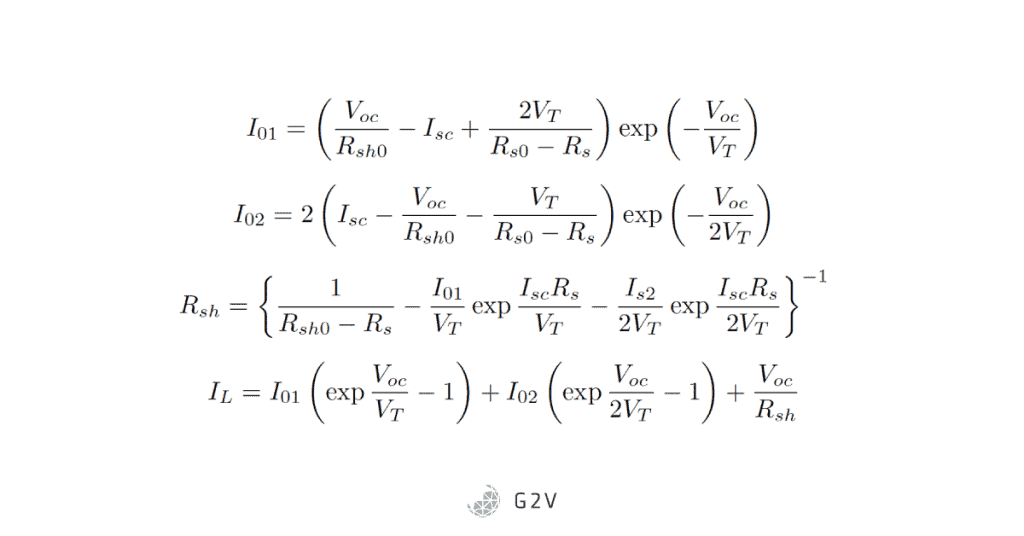
The above approximate solutions for the one-diode and two-diode models are what G2V currently uses to obtain the parameters given on the test certificates of our reference cells.
Temperature Sensitivity of IV Model Parameters
A solar cell’s performance does depend on environmental conditions, something we haven’t really discussed in detail yet. We can actually get more specific, characterizing the specific ways each of our model parameters is affected by temperature. This is probably one of the more practical complexities to introduce in order to understand or estimate a solar cell’s performance at different temperatures. The equations and trends below allow us to use measurements taken at a standard temperature to predict cell performance at other temperatures.
The photocurrent varies as follows:
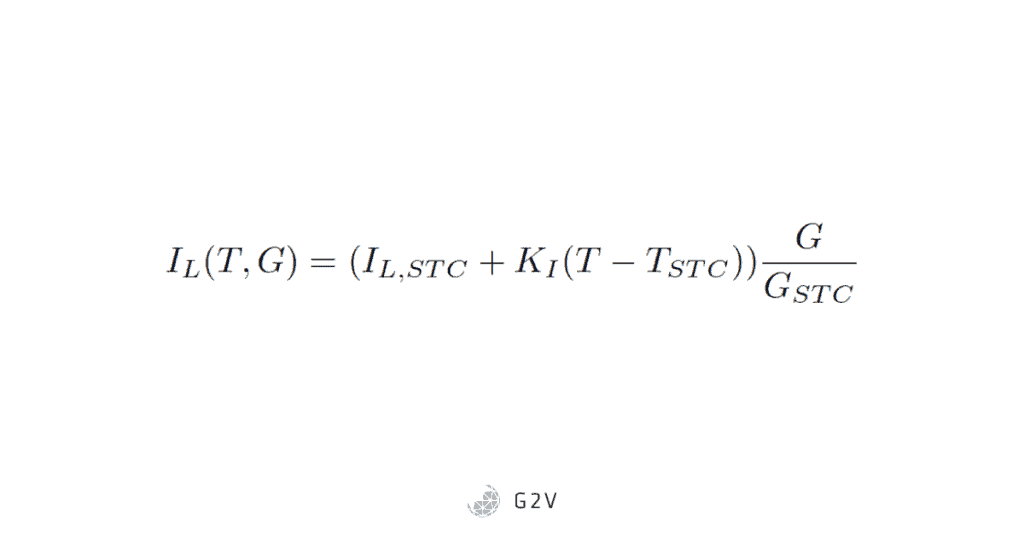
Where STC is the standard temperature condition, KI is the temperature coefficient for photocurrent, and G is irradiance.
The other solar cell parameters vary with temperature as follows:
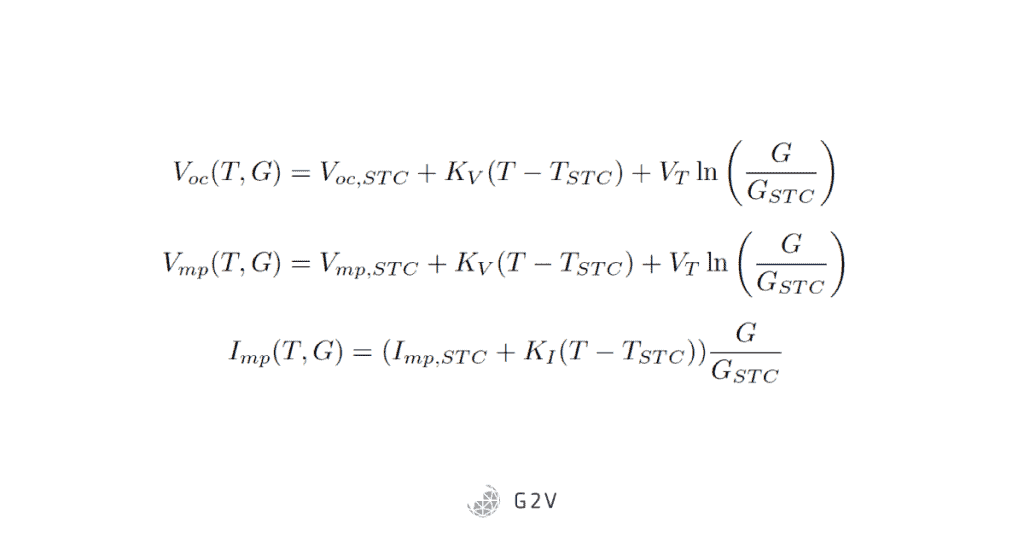
We see above that, in addition to knowledge of the parameters at a standard temperature, we also need to know the temperature coefficients for both current and voltage. These latter two values are usually determined experimentally and fit using the above equations, and many solar cell manufacturers include these coefficients in their device datasheets.
Other Circuit Models for Photovoltaic Cells
Before we discuss the numerical methods used by researchers to determine solar cell model parameters, it’s worth mentioning that other, more complex circuit models exist, and they each offer different ways of representing the fundamental device physics driving the photovoltaic cell behaviour. As with all the models, the selection is driven by the need to balance complexity with practical, communicable solutions.
| Name | Reference |
| Single-Diode Model with capacitance | Suskis P, Galkin I. Enhanced photovoltaic panel model for MATLAB-simulink environment considering solar cell junction capacitance, in: proceedings of the 39th annual conference of the IEEE industrial electronics society (IECON 2013). IEEE; 2013. p. 1613–18. DOI: doi.org |
| Three Diode Model | Nishioka K, Sakitani N, Uraoka Y, Fuyuki T. Analysis of multicrystalline silicon solar cells by modified 3-diode equivalent circuit model taking leakage current through periphery into consideration. Sol Energy Mater Sol Cells 2007;91:1222–7. DOI: doi.org |
| Modified two-diode models | Kurobe K-i, Matsunami H. New two-diode model for detailed analysis of multicrystalline silicon solar cells. Jpn J Appl Phys 2005;44:8314. DOI: ui.adsabs.harvard.edu Mazhari B. An improved solar cell circuit model for organic solar cells. Sol Energy Mater Sol Cells 2006;90:1021–33. DOI: doi.org |
| Drift-diffusion model | Lumb MP, Bailey CG, Adams JG, Hillier G, Tuminello F, Elarde VC, Walters R. Analytical drift-diffusion modeling of GaAs solar cells incorporating a back mirror. In: proceedings of IEEE 39th photovoltaic specialists conference (PVSC 2013). IEEE; 2013. p. 1063–68. DOI: dx.doi.org |
| Multi-dimension diode model | Soon JJ, Low K-S, Goh ST. Multi-dimension diode photovoltaic (PV) model for different PV cell technologies. In: proceedings of IEEE 23rd international symposium on industrial electronics (ISIE 2014). IEEE; 2014. p. 2496–501. DOI: doi.org |
Metaheuristic Example: Artificial Bee Colony for Determining PV Cell Parameters
This entire example is taken from Oliva, D., Cuevas, E., & Pajares, G.’s 2014 paper entitled. “Parameter identification of solar cells using artificial bee colony optimization,” published in Energy.

Metaheuristic approaches to PV cell parameter estimation are basically different numerical optimisation methods. The undergoing optimisation is usually to minimize the error between a given fit to the parameters, and the original data. To put this into proper context, we will go through one example algorithm known as the Artificial Bee Colony (ABC) model, which takes inspiration from the behaviour of bees as they forage for food.
Any metaheuristic approach will define an objective function which it will then seek to optimize. In the case of the Artificial Bee Colony, it seeks to minimize the root mean square error, so its objective function is as follows:

Where Ii,exp is each experimental data point for the current, and Ii,est is each estimated data point for the current.
All the parameters that are available to adjust in order to match the data are gathered together into what’s called a decision vector. The ABC method can be applied to the single-diode model, which has the following decision vector:
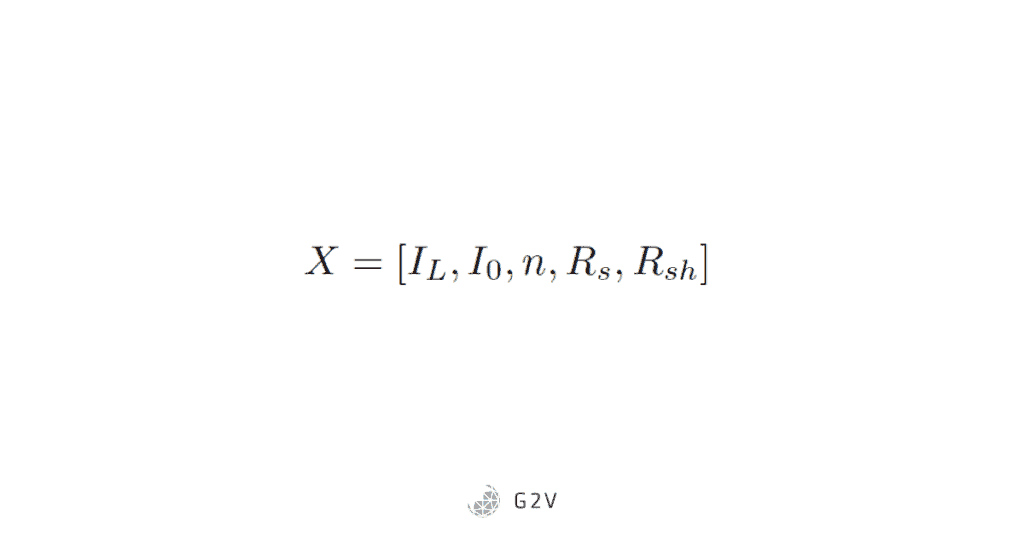
The ABC method can also be applied to the double-diode model, which has the following decision vector (sometimes the ideality factor is also included in this, though usually, the recombination diode accounts for ideality):
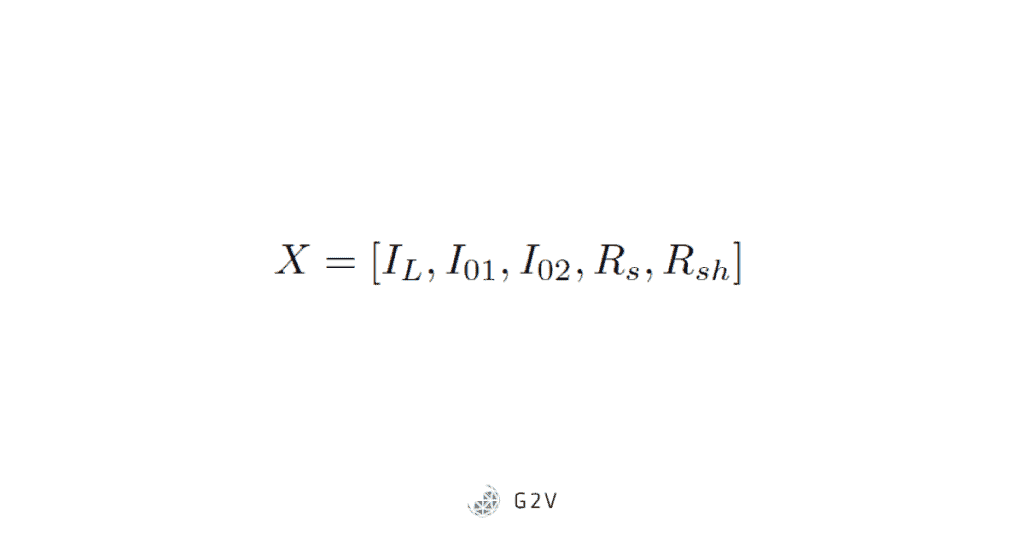
The ABC algorithm starts with a population of food sources. Each of these “food sources” is one of the decision vectors described above. Their values are randomly and uniformly distributed between a set of defined boundaries.
The following three steps are then carried out until a “finish” criterion is met:
- Send out employed bees
- Choose food sources using onlooker bees
- Determine the scout bees
The employed bees represent solution attempts, so their number is the same as the number of food sources. The employed bees are hunting for the best food sources.
Each of the employed bees takes a random step through the decision vector (all while staying within the defined boundaries). The fitness parameter (our objective function, the RMSE above) is used to determine the quality, or nectar value, of a food source. If the employed bee has found a food source (solution) with a higher nectar value than its old one, then it forgets the old source and remembers the new source. In other words, it discards its old solution and keeps the new solution.
The role of onlooker bees is to watch from a distance and see which are the best food sources before joining the rank of employed bees. In practical terms, onlooker bees are then applied to the food sources using a probability function. The food sources with a higher nectar value have a higher probability of attracting onlooker bees. The onlooker bees then become employed bees, with new food sources randomly moved from the source they were initially attracted to.
Finally, we have the scout bees. The scout bees are there to watch and make sure the employed bees don’t waste their time pursuing poor-nectar food sources. These poor-nectar food sources are considered ones that can’t be improved through a given number of trials. If a nectar source’s fitness value (RMSE, above) doesn’t improve after a specified number of times.
While the above language sounds pretty far-removed from programming, it’s a useful way to construct and articulate the coding layers and moving parts that might otherwise seem very abstract. Linking to and being inspired by biology is a common practice in many complex optimization problems.
If you’re interested in seeing how the above steps are represented by equations, they’re included below.
– For Advanced Users –
The Np food sources, each consisting of a decision vector of dimension d, are initialized as follows:
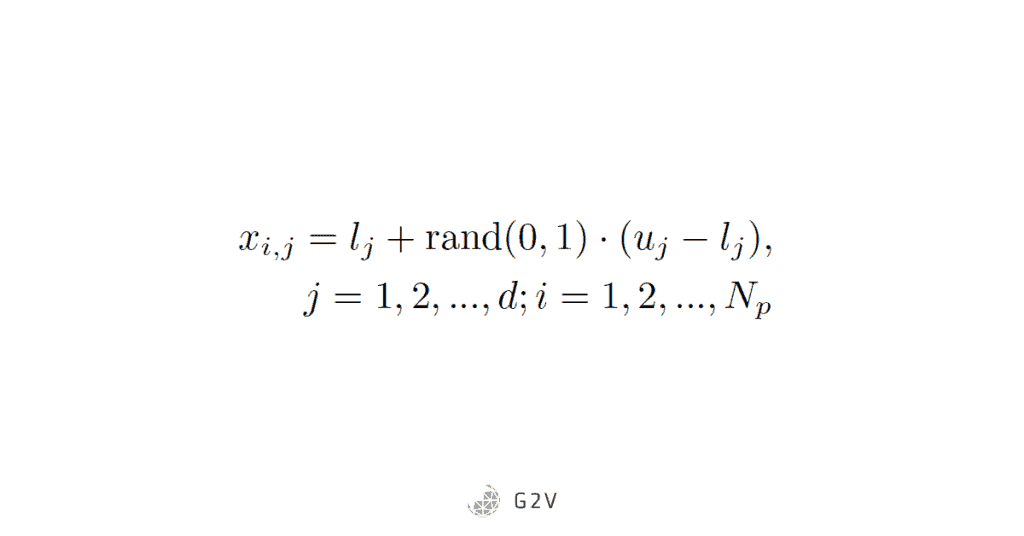
Where lj is the lower bound and uj is the upper bound, and rand(0,1) is a random decimal value between 0 and 1.
The employed bees are then moved out from the initial food sources to try and find more fruitful nectar, by moving via the following equation:
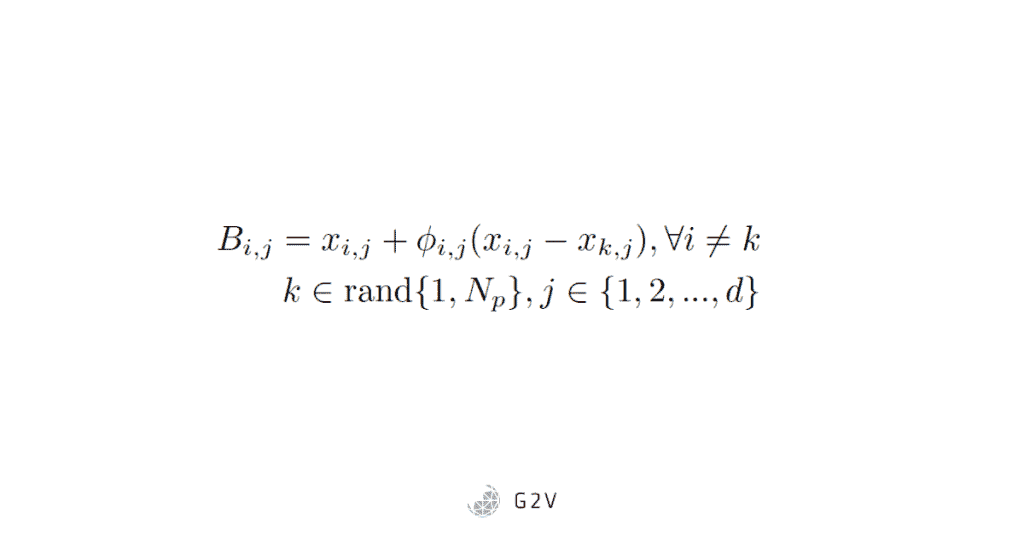
We then evaluate whether the food source the bees have food is a better one, using the following equation for “fitness”. This is a common approach for problems where we’re trying to minimize.
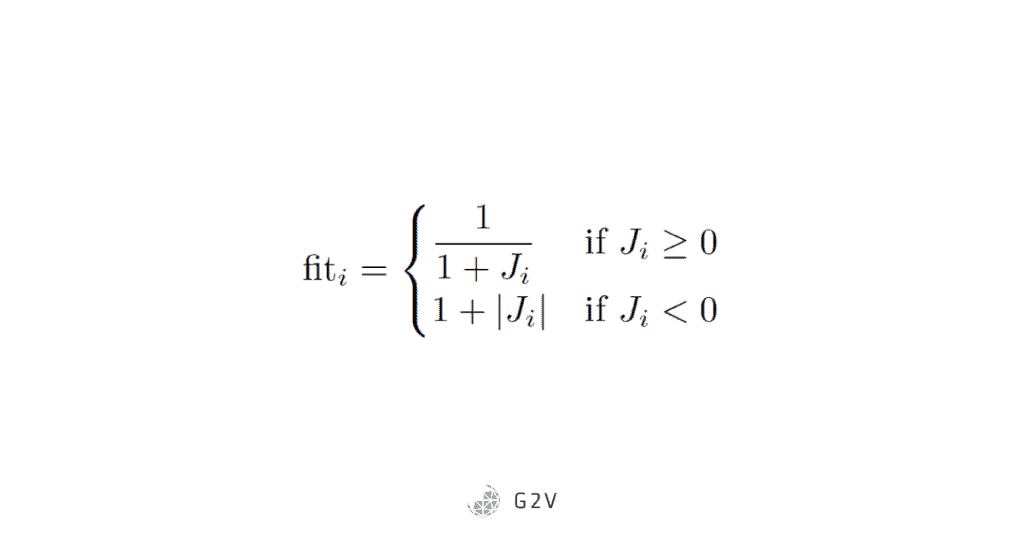
For the probability of whether or not a food source is desirable by an onlooker bee i, the following equation is used, so the food sources with a greater fitness value have a higher probability:

Other Numerical Methods for Determining PV Cell Parameters
There are a score of metaheuristic strategies employed by scientists and researchers around the world. The table below is by no means comprehensive, but provides starting references for a wide variety of approaches.
Table of Numerical Methods for Determining PV Cell Parameters, many of which were taken from a similar table in Jordehi’s 2016 review paper (see references)
| Optimization Algorithm | References |
|---|---|
| Modified artificial bee colony | Askarzadeh A, Rezazadeh A. A new artificial bee swarm algorithm for optimization of proton exchange membrane fuel cell model parameters. J Zhe- jiang Univ Sci C 2011;12:638–46. link.springer.com |
| Harmony search (HS) | Askarzadeh, A., & Rezazadeh, A. (2012). Parameter identification for solar cell models using harmony search-based algorithms. Solar Energy, 86(11), 3241–3249. doi.org |
| Particle swarm optimization (PSO) | Soon, J. J., & Low, K. S. (2012). Photovoltaic model identification using particle swarm optimization with inverse barrier constraint. IEEE Transactions on Power Electronics, 27(9), 3975–3983. doi.org |
| Genetic Algorithm (GA) | Ismail, M. S., Moghavvemi, M., & Mahlia, T. M. I. (2013). Characterization of PV panel and global optimization of its model parameters using genetic algorithm. Energy Conversion and Management, 73, 10–25. doi.org |
| Bacterial foraging optimization algorithm (BFOA) | Rajasekar, N., Krishna Kumar, N., & Venugopalan, R. (2013). Bacterial Foraging Algorithm based solar PV parameter estimation. Solar Energy, 97, 255–265. doi.org |
| Simulated Annealing (SA) | El-Naggar, K. M., AlRashidi, M. R., AlHajri, M. F., & Al-Othman, A. K. (2012). Simulated Annealing algorithm for photovoltaic parameters identification. Solar Energy, 86(1), 266–274. doi.org |
| Differential Evolution (DE) | Jiang, L. L., Maskell, D. L., & Patra, J. C. (2013). Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm. Applied Energy, 112, 185–193. doi.org |
| Adaptively-controlled scaling factors and crossover rates | Muhsen DH, Ghazali AB, Khatib T, Abed IA. Extraction of photovoltaic module model’s parameters using an improved hybrid differential evolution/electromagnetism-like algorithm. Sol Energy 2015;119:286–97. DOI: doi.org |
| Penalty-based DE | Ishaque K, Salam Z, Mekhilef S, Shamsudin A. Parameter extraction of solar photovoltaic modules using penalty-based differential evolution. Appl Energy 2012;99:297–308. DOI: doi.org |
| DE with adaptive strategy for scaling factor and crossover rate | Jiang LL, Maskell DL, Patra JC. Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm. Appl Energy 2013;112:185–93. DOI: doi.org |
| Improved version of JADE | Gong W, Cai Z. Parameter extraction of solar cell models using repaired adaptive differential evolution. Sol Energy 2013;94:209–20. DOI: doi.org Zhang J, Sanderson AC. JADE: adaptive differential evolution with optional external archive. Evolut Comput IEEE Trans 2009;13:945–58. DOI: doi.org |
| Linearly decreasing inertia weight PSO | Khanna V, Das B, Bisht D, Singh P. A three diode model for industrial solar cells and estimation of solar cell parameters using PSO algorithm. Renew Energy 2015;78:105–13. DOI: doi.org |
| Pattern Search | AlRashidi M, AlHajri M, El-Naggar K, Al-Othman A. A new estimation approach for determining the I–V characteristics of solar cells. Sol Energy 2011;85:1543–50. DOI: doi.org AlHajri M, El-Naggar K, AlRashidi M, Al-Othman A. Optimal extraction of solar cell parameters using pattern search. Renew Energy 2012;44:238–45. DOI: doi.org |
| BBO with chaotic-based mutation strategy | Niu Q, Zhang L, Li K. A biogeography-based optimization algorithm with mutation strategies for model parameter estimation of solar and fuel cells. Energy Convers Manag 2014;86:1173–85. DOI: doi.org |
| Innovative global harmony search (IGHS) | Askarzadeh A, Rezazadeh A. Parameter identification for solar cell models using harmony search-based algorithms. Sol Energy 2012;86:3241–9. doi.org |
| Bird mating optimisation | Askarzadeh A, Rezazadeh A. Extraction of maximum power point in solar cells using bird mating optimizer-based parameters identification approach. Sol Energy 2013;90:123–33. DOI: doi.org |
| Flower pollination algorithm | Alam D, Yousri D, Eteiba M. Flower pollination algorithm based solar PV parameter estimation. Energy Convers Manag 2015;101:410–22. DOI: doi.org |
| Modified TLBO | Niu Q, Zhang H, Li K. An improved TLBO with elite strategy for parameters identification of PEM fuel cell and solar cell models. Int J Hydrog Energy 2014;39:3837–54. DOI: doi.org |
| Modified version of chaos optimisation algorithm | Yuan X, Xiang Y, He Y. Parameter extraction of solar cell models using mutative-scale parallel chaos optimization algorithm. Sol Energy 2014;108:238–51.DOI: doi.org |
| SA hybridized with Levenberg-Marquardt (LM) | Dkhichi F, Oukarfi B, Fakkar A, Belbounaguia N. Parameter identification of solar cell model using Levenberg–Marquardt algorithm combined with simulated annealing. Solar Energy 2014;110:781–8. DOI: doi.org |
| Artificial Immune System (AIS) | Jacob B, Balasubramanian K, Azharuddin SM, Rajasekar N. Solar PV modelling and parameter extraction using artificial immune system. Energy Procedia 2015;75:331–6. DOI: doi.org Jacob B, Balasubramanian K, Babu TS, Rajasekar N. Parameter extraction of solar PV double diode model using artificial immune system. In: proceedings of IEEE international conference on signal processing, informatics, communication and energy systems (SPICES 2015); 2015. p. 1–5. DOI: doi.org |
Hybrid Algorithm Example: Genetic Algorithm for Determining Solar Cell Parameters
The following example is taken from Jiang, L. L., Maskell, D. L., & Patra, J. C.’s 2013 paper entitled “Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm,” in Applied Energy.
Our hybrid algorithm example, as we’ve mentioned above, combines analytical solutions with iterative numerical approaches. Genetic algorithms are a broad class of methods that have been used to solve both constrained and unconstrained optimization problems.
The general approach is that there is a population of individuals who are repeatedly modified, and at each step, a group is randomly selected to be parents of the next generation.
There are three main rules used to form the next generation:
- Selection rules: those that select the parents
- Crossover rules: those that combine two parents to make a baby
- Mutation rules: those that randomly apply changes to individuals.
If the genetic algorithm were used by itself to generate solutions for the IV curve parameters, then it would be an entirely numerical, metaheuristic approach. However, what the researchers in this example did was to evaluate a variety of scenarios where some parameters were determined by solving the equations analytically (similar to the methods discussed in the one and two-diode model sections), while the remainder were then found using a genetic algorithm. In one case, they determined most of the parameters of the decision vector through analytic means, then used the genetic algorithm to calculate the ideality factor, the series resistance, and the parallel resistance.
Such combined approaches allow the minimization of computational resources while maximizing the accuracy of the obtained parameters.
Other Hybrid Strategies for Determining Solar Cell Parameters
There are many other hybrid strategies employed by researchers. Some of the ones that use the single-diode model have been assembled in the table below for reference.
Table of Numerical Methods for Determining PV Cell Parameters from Jordehi’s 2016 review paper (see references)
| Optimization Algorithm | Reference |
|---|---|
| Differential Evolution & others | Ishaque K, Salam Z. An improved modeling method to determine the model parameters of photovoltaic (PV) modules using differential evolution (DE). Solar Energy 2011;85:2349–59. DOI: doi.org |
| Linearly decreasing inertia weight particle swarm optimization | Soon JJ, Low K-S. Photovoltaic model identification using particle swarm optimization with inverse barrier constraint. Power Electron IEEE Trans 2012;27:3975–83. DOI: doi.org |
| Hybrid of Genetic Algorithm and interior point | Dizqah AM, Maheri A, Busawon K. An accurate method for the PV model identification based on a genetic algorithm and the interior-point method. Renew Energy 2014;72:212–22. DOI: doi.org |
| Pattern search | Park J-Y, Choi S-J. Datasheet-based circuit parameter extraction method for maximum power point simulation of photovoltaic array. In: proceedings of the 9th international conference on power electronics and ECCE Asia (ICPE- ECCE Asia 2015). IEEE; 2015. p. 1413–19. DOI: doi.org |
| Bacterial Foraging Optimisation Algorithm | Rajasekar N, Kumar NK, Venugopalan R. Bacterial foraging algorithm based solar PV parameter estimation. Sol Energy 2013;97:255–65. DOI: doi.org |